|
|
|
J'ai animé en 2011-2012 des ateliers
de circonscription sur le thème du jeu et des apprentissages
mathématiques. Cette page fut d'abord le reflet du travail mis en
place. Puis je décidai, à la fin de l'année universitaire, d'étoffer
mes propositions.
En 2012-2013 j'anime à nouveau des ateleirs sur ce thème, ce qui
m'amène à faire évoluer encore cette page.
|

|
 |
Cet onglet présente divers jeux que les
participants aux ateliers de circonscription ont eu loisir d'étudier
sous ma houlette. Je leur avais adjoint de nombreux modules logiciels
d'accompagnement.
Certains fonctionnaient en ligne. Malheureusement, la technique
employée est devenu obsolète, ce qui m'a obligé à revoir cette page en
2013. Ce faisant, j'en ai profité pour faire évoluer certaines
propositions.
L'onglet [Points de repère] énonce certains éléments théoriques assez
classiques, en s'appuyant sur les jeux ici présentés. Enfin, j'ai
glissé dans l'onglet [Web/Biblio graphie] les ressources documentaires
qui me semblaient incontournables ou dignes d'une visite. |
 |
J'avais distribué
un document(-papier) aux participants de ces ateliers ; vous pouvez en
prendre connaissance en cliquant sur la vignette ci-contre à droite.
La présentation ci-dessous ne reprend pas son ordonnancement.
Je préfère ici organiser mon texte autour de questions que l'on est
amené naturellement à se poser quand on réfléchit sur le thème du Jeu à
l'école primaire dans le cadre des apprentissages mathématiques.
Ce que vous allez lire ci-dessous double donc le document initial,
mais en le complétant. |
 |
En effet, chaque fois que possible, je fournis des moyens -informatiques-
de présenter au groupe-classe le jeu étudié.
Je suppose ainsi que vous
disposez d'un vidéoprojecteur voire d'un TNI.
Il peut s'agir de simples fichiers réalisés avec le module de dessin
vectoriel de la suite Open Office (ou Libre Office). Pour vous en
servir, vous devez maîtriser quelques gestes simples : changer de page
grâce au volet [Pages] , déplacer une forme (jouant le rôle de jeton),
mais rien de plus !
Concernant le chargement de
tels fichiers, lire attentivement la note en vert ci-dessous.
Il peut aussi s'agir de petits logiciels de simulation, pour PC sous
Windows uniquement. Sauf pour le jeu du pion empoisonné,
il s'agit de maquettes qui permettent à deux joueurs (ou deux équipes)
d'intervenir à tour de rôle. Le programme simule donc les éléments du
jeu réel, qui sera mis en
circulation par ailleurs. Par la suite, les deux dispositifs,
informatique sur un PC en fond de classe et manuel, peuvent tout à fait
coexister.
Les logiciels proposés ici sont téléchargeables directement
(parfois sous forme d'archives à décompresser). En tous cas, il
n'y a jamais d'installation à faire. Mes simulateurs sont fournis
pour le système Windows. Dans certains cas, je dispose d'une version
pour Mac OS X ou Linux. M'écrire en profitant du bouton [Contact] tout
en haut de cette page.
Sauf mention contraire, tous
les fichiers proposés sont librement utilisables, sauf à des
fins commerciales. Il va
sans dire que je garde l'intégralité de mes droits d'auteur sur ces
fichiers.
|

|
 |
Modification
2013 importante : Pendant un temps, il fut possible de charger
une version en ligne de certains de mes petits modules. La technologie
employée supposait le chargement d'un pluggin conçu par la société RunRev. Malheureusement, cette technologie
n'est plus supportée. Je me contente donc de vous proposer une copie
d'écran du jeu en cours de partie. |
Si je peux trouver une
solution, les jeux en ligne retrouveront leur place sur ma page.
|
| Qu'attend-on d'un jeu ? |
 |
|
 |
Voici six jeux qui me semblent très
intéressants en soi, et sauf le dernier peut-être, à la portée d'élèves
de l'école primaire. Certaines
capacités sont nécessaires : aptitude à se déplacer sur un réseau,
prise en compte de l'adversaire, résistance, imagination. Bien que jeux
de plateau et avec jetons, ils sont tous très différents. Mais
qu'apporte-t-on aux enfants en proposant ces jeux ? |
 |
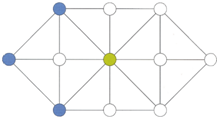
Léa
et les pirates
{CE - CM} 2 joueurs. Sur un plateau de jeu présentant un
réseau à 11 n?uds on dispose 3 pions bleus (les pirates) et 1 pion vert
(Léa) comme illustré ci-contre. Le but du jeu pour les pions bleus est
de bloquer le jeton vert.
Il s'agit donc d'un jeu de mérelle et plus particulièrement d'un jeu
dit "du voleur et des gendarmes". |
 |
|
|
Ces jeux sont modélisés par la
théorie des Graphes. Bien entendu, de telles modélisations n'ont pas
leur place ici. Ce jeu s'est aussi appelé "Jeu Militaire" ; il
a eu beaucoup de succès en France vers la fin du 19ième siècle. Martin
Gardner vantait ce jeu pour la simplicité de ses règles et son extrême
subtilité. |
|
Rappelons les règles de ce jeu : le jeton vert peut visiter toute
case voisine libre ; les jetons bleus, qui ne se déplacent qu'à tour de
rôle, ne peuvent qu'avancer vers la droite. Le joueur responsable du
jeton vert perd si son jeton est bloqué.
Dans une variante, on permet au jeton vert de se placer où bon lui
semble en début de partie.
Une autre variante, qui sera développée ci-dessous, consiste en la
clause de non-retour : le jeton vert ne peut pas revenir sur la
position occupée le coup précédent. |
 |
|
|
Vous trouverez plus d'indications
dans la brochure Atelier_DB ... pdf . Pour présenter le jeu à la
classe, ce qui suppose que vous disposez d'un vidéoprojecteur,
n'hésitez pas à utiliser mon petit module oOo Draw : Cliquez sur la
vignette ci-dessus à droite pour charger le fichier. Puis vous
l'ouvrirez avec Libre Office ou Open Office. Je suppose que vous maîtrisez les
rudiments les plus basiques de ce genre de logiciel. Le
fichier comprend deux pages. Jouez sur la première page. Si vous voulez relancer une nouvelle
partie, en profitant
du volet [Pages], affichez la dernière page puis dupliquez-la. Revenez ensuite sur l'avant-dernière
page et commencez à jouer.
Cette façon de pratiquer
peut se révéler utile pour comparer des éléments tactiques. |
|
 |
Repérez
les lignes et colonnes bleutées ainsi que leurs étiquettes : elles
doivent permettre aux élèves de déclarer facilement la position des
jetons et donc de décrire des éléments de partie.
Vous
pouvez aussi faire jouer les enfants sur des plateaux de jeu faits
main. Vous trouverez ci-contre un fichier au format Pdf
permettant d'imprimer deux planches de jeu. Il ne vous restera plus
qu'à plastifier et massicoter.
|
|
|
Notez
que les jetons ne sont pas fournis !
Des
capsules de bouteilles d'eau feront parfaitement l'affaire. On
en trouve aussi bien des vertes que des bleues ! La question
qui taraude est bien entendu "Qui gagne ? Et comment ?".
Il a été démontré que si les bleus commencent la partie et jouent
rationnellement, alors ils doivent gagner. Mais la stratégie à
appliquer n'est pas simple, en sorte qu'un bon joueur tenant le trait
vert peut gagner contre le joueur tenant les bleus. |
 |
|
|
Pour raccourcir le
temps de jeu, on peut ajouter une clause de non retour. Cette clause
facilite aussi l'analyse du jeu.
Cliquez sur la vignette
ci-dessus à droite pour charger un fichier d'étude d'une douzaine de
pages.
Certains éléments sont assez techniques et vous en sauterez sans doute
la lecture. Je vous recommande cependant la lecture des pages 5 et 6 de mon
opus.
La conclusion est la
suivante : si Bleu commence, Bleu gagne, si Vert commence, Vert
peut au mieux obtenir le pat.
|

|
Le jeu "Léa et les
Pirates" appartient à la grande famille des jeux de chasse. Ici il n'y
a pas prise mais juste immobilisation.
Tel n'est pas le
cas du jeu "Le renard et les poules
(ou les oies)" puisque le renard prend, tandis que les poules
essayent de rester groupées pour immobiliser le renard.
Ce jeu est très
ancien et de nombreux sites médiévalistes en font leurs choux-gras.
 |
Ce jeu à deux joueurs nécessite un
plateau, 13 jetons symbolisant les poules (17 dans une variante) et un
jeton représentant le renard.
On peut se contenter d'un plateau de solitaire anglais tel qu'illustré ci-contre à
gauche. On peut aussi
fabriquer soit même des plateaux de jeu, voire les faire produire par
les élèves.
On privilégie en ce cas des plateaux
en forme de croix comportant 33 n?uds. Cette croix se décompose en 5 carrés
de 9 n?uds se recouvrant partiellement. Le tracé est à la portée des
élèves de cycle 3. |
|
|
Vous trouverez dans le fichier Renard&Poule(2plateaux).pdf
une première planche expliquant les règles du jeux puis
une planche au format A4 proposant deux plateaux de jeux et des jetons.
Imprimez cette planche, plastifiez puis découpez ses éléments.
Les jetons, circulaires, ont un diamètre de 1,5 cm. On peut les coller
sur des jetons cylindriques achetés en nombre : Sans vouloir
privilégier ce site, voir sur le site de toutpourlejeu.
Pour présenter le jeu, j'ai conçu un petit module Libre Office Draw (en
attendant mieux).
|
Attention : ce fichier est
uniquement destiné à la vidéo-projection, pas à une impression.
Au format A5 en mode
paysage, la première page du fichier affiche un plateau de jeu sur
lequel on peut déplacer les jetons. Avant de lancer une partie,
dupliquez cette première page. Quand cette partie est terminée,
supprimez la page courante, et reprenez la procédure précédente. Vous
ne devez en aucun cas enregistrer les modifications du fichier originel.
La seconde page du fichier (qui peut glisser en troisième position)
rappelle les règles du jeu.
Pour charger ce fichier,
cliquez sur la vignette ci-dessus à gauche, ou cliquez ici.
Repérez sur le plateau de jeu les étiquètes de lignes ou
de colonnes. Elles facilitent l'identification des positions à quitter
ou à atteindre.
|
 |
Pas Japonais et Caillebotis
{GS à CE} 2 joueurs.
Ces deux jeux ont la même structure de base, en forme de quadrillage,
et le même principe de jeu : à tour de rôle, chacun des 2 joueurs
accroche une pièce à un chemin, qu'il vient donc prolonger et une
pièce condamnant une cellule du quadrillage. Ces jeux sont donc des
jeux de cul de sac. |
 |
|
|
L'habillage change
d'un jeu à l'autre, comme les règles de pose qui varient légèrement,
rendant le jeu "Caillebotis" un peu plus facile ...
Pour une première impression de l'habillage de chaque jeu, cliquez sur
l'une des deux vignettes ci-dessus à droite.
Mais le plus simple reste sans doute que vous chargiez puis
décompressiez l'archive ci-dessous.
Attention : 3,5 Mo à
charger.
Vous lirez dans mon
document "Deux jeux de cul_de_sac.pdf" une présentation complète de ces
jeux et une analyse rapide des difficultés rencontrées par de jeunes
enfants.
Enfin, à condition de disposer de jetons adaptés (2 sortes) pourquoi ne
pas fabriquer des plateaux de jeu manuel ? |
 |
 |
 |
|
 |
Jeu du Kono {CE à CM} 2
joueurs
Il s'agit d'un petit jeu de damier, originaire de Corée, où il faut
jouer à saute mouton avec ses propres pions pour pouvoir capturer ceux
de l'adversaire. L'espace du jeu consistant en un quadrillage de 4x4
cases assure un temps de jeu limité. Contrairement aux deux jeux
présentés ci-dessus, on peut voir les enfants développer sinon une
réelle pensée stratégique, du moins des éléments de tactique. |
|
|
| Vous trouverez sur le site jeuxstrategieter.free.fr
une présentation du jeu, j'en ai extrait l'imagette ci-dessus. Ce jeu
est aussi cité par le site des animations Francas de Pau, sur lequel
j'ai prélevé la règle du jeu proprement dite. Profitez de la
seconde icône ci-contre à droite pour la consulter, mais que cela ne
vous empêche pas de visiter le site palois.; vous y trouverez en effet
de nombreux jeux de plateau, des plus intéressants quoique classiques
et faciles à reproduire. |
 |
 |
 |
Pour me faciliter la
présentation de ce jeu, j'avais programmé un petit logiciel. Celui-ci
se contente d'indiquer qui doit jouer et de contrôler la validité du
coup. En revanche, l'ordinateur ne joue pas. Téléchargez l'archive
(icône ci-dessus) puis décompressez la. Pour jauger de suite de
l'intérêt ou non de mon module, ouvrez le fichier pdf présentant un
exemple de partie, en cliquant sur la troisième icone ci-dessus tout à
droite.
Il est évidemment
très rapide de dessiner un quadrillage de 4x4 cases.
 |
On peut aussi choisir de mettre à
disposition des élèves un tel terrain de jeu. Le fichier
Plateaux_Kono(A4).pdf y pourvoit. Vous y trouverez deux planches au
format A4, en 300 dpi. La première propose 4 plateaux de jeu. Les cotés
des cases de ces plateaux mesurent 2,2 cm environ. Si ces cases vous
semblent trop petites, optez pour la seconde planche. Cette dernière
offre deux plateaux compatibles avec les jetons usuels du jeu de dames.
On peut substituer à ces jetons des bouchons d'eau minérale. Choisissez
la planche qui convient à votre projet, imprimez, plastifiez
découpez ...
|
|
 |
Jeu du Pogo {CM ...} 2
joueurs dont l'ordinateur
Il s'agit d'un jeu de prise. Il utilise le plus petit terrain (un carré
3 x 3) que je connaisse. Le principe est simple: il s'agit de capturer
les pions de l'adversaire en les coiffant avec les siens. |
 |
|
|
Le jeu fut initialement édité en
coffret avec de jolis pions en bois s'incrustant bien les uns sur les
autres (Clic sur l'imagette ci-dessus).
Maintenant le logiciel n'existe plus
que sous forme logicielle. A priori, on joue en premier et
l'ordinateur répond, mais on peut inverser les rôles. Vous
trouverez les règles du jeu sur www.nivozero.com. Profitez de la visite sur ce site
pour y lire les conseils pour bien débuter. Et soyez patient, car on
perd toujours les premières parties !
Le logiciel a été programmé en Java. Si vous avez un MAC, Pogo ne
fonctionnera que sous OsX. Sur un PC, Java doit être installé. Vous
trouverez Java sur la pagne http://java.com/fr/. |
 |
Vous pouvez télécharger ce
jeu depuis le site propriétaire comme vous pouvez rapatrier l'archive
depuis cette page pour la décompresser : cliquez sur la vignette
ci-dessus à droite. |
 |
Un premier bilan
Quels sont les jeux que
vous retiendriez pour les présenter à vos élèves ? Dans quel but le
feriez-vous ? Selon quelles modalités ? Si vous avez l'impression qu'aucun de
ces jeux n'est compatible avec les programmes en cours, peut-être la
partie suivante vous conviendra-t-elle mieux. |
| Jeux de calcul rapide |
 |
|
 |
Voici
5 jeux à nouveau, mais dans le champ numérique cette fois.
Brrr ! Quitterions-nous le rivage du jeu à l'état pur pour celui des
apprentissages ? |
 |
Jeu
du Chat et de la Souris {CE} 2 joueurs.
Un jeu très ancien puisque proposé par la brochure n°59 de la
revue de l'APMEP, datant de 1983.
Il s'agit d'un jeu de poursuite sur la droite numérique entre deux
joueurs, le chat et la souris. Au début du jeu, la souris est en "30"
et le chat sur "1". C'est la souris qui commence. |
 |
|
|
Le but de la souris est de se
réfugier en "0". Elle y parvient en reculant (ou en avançant) d'un
nombre entier de pas compris entre 1 et 9. Le but du chat est de
rattraper la souris en avançant (ou en reculant) d'un nombre entier de
pas compris entre 1 et 9. Vous
trouverez un descriptif complet à la page 2 de ma brochure
Atelier_DB ... pdf .
Pour mes besoins propres, j'ai programmé un petit démonstrateur :
l'ordinateur demande alternativement à la souris puis au chat de jouer,
tout en contrôlant la validité du coup et la fin de partie.
L'ordinateur ne joue pas. |
 |
Pour un aperçu du jeu
électronique, cliquez sur l'imagette ci-dessus à droite. Si
vous disposez d'un PC, vous pouvez charger l'archive "JCS.zip", puis
après décompression, déposer le dossier contenant mon petit programme
où bon vous semble : comme déjà indiqué, il n'y a pas d'installation à
prévoir.
 |
Mon travail appelle une remarque
: dans le jeu papier-crayon, une feuille de marque est distribuée aux
élèves ou préparée par eux. Cette feuille de marque affiche les
entiers qui seront utilisés (chaque joueur barre dans sa colonne
l'entier choisi). Mais la feuille affiche aussi une colonne par joueur
dans laquelle les résultats successifs des calculs sont énoncés, ce qui
permet entre autres de contrôler les résultats partiels. En revanche
les nombres choisis n'apparaissent pas en regard du résultat qu'il a
engendré. {Cliquez sur l'imagette ci-contre à gauche pour
afficher un exemple de feuille de marque.} |
Mon
logiciel enregistre les opérateurs mobilisés et tient à jour la
position de chaque joueur sur la droite numérique, sans dresser le
listage des positions intermédiaires. Dit autrement, les calculs
intermédiaires n'apparaissent pas. Aux joueurs de les retrouver.
|
 |
Le quinze vainc
(CE à CM) 2 joueurs
Ce jeu, inventé par Martin Gardner (1914-2010) connait plusieurs
formes. Dans la version initiale deux joueurs s'affrontent sur une
grille de 9 cases, numérotées de 1 à 9. Chacun d'eux dispose de 3
jetons à sa couleur. Les jetons sont posés un par un et à tour de rôle
par les joueurs, puis peuvent éventuellement glisser sur des cases
inoccupées. Le but du jeu est de faire 15. |
 |
|
|
| Pour la présentation en classe, vous
pouvez-vous contenter d'afficher au tableau une bande numérique et
disposer deux groupes de 3 aimants colorés comme sur la proposition
issue de l'Inspection du Haut-Grésivaudan (Cf. illustration
ci-contre). |
 |
 |
Vous pouvez aussi faire appel (sur PC
uniquement) à ma petite simulation "simul1524.exe" en cliquant sur la
vignette ci-dessus à droite. Pour un exemple de partie en cours,
cliquez sur l'imagette ci-contre à gauche.
Mon programme, se
contente d'attendre l'intervention d'un joueur puis d'un autre. Le
programme intervient si peu qu'il ne reconnaît même pas qui gagne.
C'est un pis-aller, qui rend des services. |
Vous trouverez en page 3 de ma brochure
Atelier_DB
... pdf un
descriptif complet de ce jeu.
Le jeu est
tellement simple à préparer que les élèves de cycle 3 peuvent aisément
dessiner le plateau de jeu. Si on est
perfectionniste, on peut s'inspirer de la proposition ci-contre.
Les disques blancs
ont un diamètre de 2,5 cm.
|
|
Mais il existe une autre version.
On peut par exemple décider que les jetons posés ne bougent pas, mais
que chaque joueur détient 5 jetons dorénavant. Le premier joueur qui
peut faire 15 avec trois de ses jetons posés a gagné. Le jeu n'est pas
symétrique.
C'est selon ce principe que fonctionne le jeu en ligne proposé par Thérèse Eveilleau.
Une déclinaison manuelle est
la suivante : on pose sur la table neuf cartes numérotées de 1 à
9. Chacun des deux joueurs choisit à son tour une carte. Le premier des
deux qui peut présenter une série de 3 cartes dont la somme des valeurs
fait 15 a gagné.
 |
Si vous jouez contre le programme de
Thérèse Eveilleau, vous serez surpris(e) par la facilité avec laquelle
l'ordinateur gagne. Il existe en effet une stratégie gagnante, et si
vous ne la connaissez pas, le mieux que vous pourrez obtenir c'est
"partie nulle" ! La raison
principale tient à un transfert de modèle.
Toutes les façons de faire 15 en sommant trois entiers différents
choisis dans la suite de 1 à 9, peut-être représentée par un carré magique, tel celui illustré ci-contre à
gauche. |
Choisir sans remise une carte
numérotée de 1 à 9 dans une pioche est équivalent à poser un jeton à sa
couleur sur le carré magique. Faire 15 avec 3cartes glanées dans la
pioche équivaut à réaliser un alignement à sa couleur sur le carré
magique.
Le jeu du "15 vainc" dans sa deuxième
version est donc équivalent à un jeu de Tic-Tac-Toe (alias Morpion 3x3), et on sait qu'il
existe une stratégie non perdante pour celui qui joue en premier. |
|
Pour
permettre à vos élèves de tester ce nouvel habillage du jeu du 1520,
profitez du fichier Libre Office KarMagik.odg. Il vout suffit de
cliquer sur la vignette ci-dessus à droite Chaque joueur dispose de 3
jetons à sa couleur (translucides) qu'il placera ou déplacera quand ce
sera son tour de jouer.
La question devient alors
: Peut-on amener les élèves d'un CM 2 à se forger les bases d'une
stratégie en s'appuyant sur l'outil des carrés magiques ? Serge Petit s'est posé cette question en 2005 ;
vous lirez sa réponse dans un
extrait du bulletin 458 de l'APMEP relatif à ce jeu.
|
 |
Computix (CE)
2 joueurs
Ce jeu pour 2 joueurs a été proposé en 1994 par Pascal Pluchon.
Pascal Pluchon n'a pas cessé de maintenir une
version pour Mac. |
 |
|
|
Cliquez sur la
vignette ci-dessus à droite pour télécharger la dernière version
-gratuite- pour Mac depuis l'AppStore. Il n'y a pas de version PC
malheureusement et vous devrez donc vous contenter de mon travail
pauvret. |
|
Le jeu fait appel à
des grilles carrées comportant un nombre impair de lignes et de
colonnes (il faut disposer d'une case au centre). Chaque cellule de la
grille retient un nombre. Le
premier joueur joue sur les lignes et le second sur les colonnes. A
tour de rôle, chaque joueur sélectionne une case sur la ligne ou la
colonne disponible. Il en prélève le contenu et l'ajoute à son propre
total. Vous trouverez en
page 5 de ma brochure Atelier_DB ... pdf un descriptif complet de ce jeu. |
|
 |
Pour
une présentation en classe, n'hésitez pas à charger mon module
(Window uniquement) Computix56.exe en cliquant sur la vignette
ci-contre à droite. Le logiciel permet à 2 joueurs de s'affronter
(l'ordinateur ne joue pas vraiment) sur des carrés 5x5 ou7x7. On
peut aussi choisir la nature (positif ou négatif) et la taille des
nombres sur une échelle graduée de 1 à 5. Enfin on peut choisir à tout
moment de masquer certaines cases (en affichant un "?"). |
 |
Passé la présentation en
grand groupe, il est vraisemblable que le jeu basculera en mode
papier-crayon.
Le fichier COMPUTixDOC.pdf
rappelle les règles du jeu puis propose quelques variantes. Le dessin
d'une grille puis son remplissage sont à portée d'élèves du Cycle 3.
Les questions posées par ce
jeu sont : quelles notions mathématiques se trouvent vraiment
engagées par ce jeu ? Faut-il vraiment effectuer des calculs pour bien
jouer ? Le hasard ne joue-t-il pas un trop grand rôle ? |
 |
A vos baguettes (CE)
2 joueurs
Jeu trouvé dans la brochure de l'IRDP mentionnée ci-dessus. Après
tirage au sort avec 2 dés, on dispose p baguettes verticalement
et q baguettes horizontalement. Le nombre de croisements
correspond ainsi au produit p x q. |
A tour de rôle, chaque
joueur ajoute ou enlève une baguette, horizontalement ou verticalement,
tout en énonçant le produit marqué et son résultat. Le joueur qui se
trompe ou qui énonce un résultat déjà fourni a perdu. La conduite de ce
jeu suppose certainement la tenue d'une feuille de marque. Vous
trouverez à la page 4 de ma brochure
Atelier_DB
... pdf quelques
remarques
supplémentaires sur ce jeu.
Il est loisible d'adapter ce
jeu en un jeu de plateau !
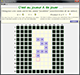
Nous
appellerons Jeu du Chemin Pythagore
ce jeu.
En voici le principe : un tableau de n par n cases contient la
table de multiplication de [1, n] par [1, n]. Toutes les cases sont
masquées, sauf une.
Le but du jeu est de
construire un chemin à partir de cette case, selon diverses
contraintes. Celui qui ne peut plus jouer a perdu. Les contraintes sont : désigner
correctement une case jouable
en énonçant ses coordonnées (col, lig) et sa valeur (produit col x
lig). Une case est jouable
parce que :
1/ elle est adjacente à la dernière case nommée,
mais 2/ elle ne jouxte pas
une case nommée antérieurement.
Cette contrainte, qui n'est pas sans
rappeler celle du jeu du Pas Japonnais permet
d'écourter la durée du jeu. J'ai écrit un petit
démonstrateur de ce jeu.
Cliquez sur l?icône ci-contre à droite pour en avoir un pâle reflet..
Pour tester mon démonstrateur (pour PC uniquement)
cliquez sur l?icône en bout de ligne. |
 |
 |
|
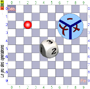 |
Le jeu des opérations (CE2/CM1)
2 joueurs
Ce jeu -très classique- voit s'affronter deux joueurs sur un plateau
10x10. Les cases sont numérotées de (0, 0) à (9, 9). Un jeton circule
sur le plateau au gré des joueurs. Deux dés, ou équivalent, sont par
ailleurs nécessaires. |
|
|
Principe
du jeu : A tour de rôle, chaque joueur tire le nombre de cases
que le jeton doit parcourir (entre 1 et 3) et l'opération à effectuer.
Le joueur déplace le jeton, repère les coordonnées de la case atteinte
puis effectue le calcul requis. Le
résultat obtenu est alors ajouté au score du joueur.
La partie se termine quand :
1/ le jeton est arrivé sur
la case (9, 9)
ou 2/ chaque joueur a effectué 10 calculs.
Vous trouverez une présentation complète du jeu, soit à la page 6
de ma brochure
Atelier_DB ... pdf , soit dans la fiche "jeu des
opérations.pdf" {ou, cliquez sur la vignette ci-contre à droite.}
|
 |
Le jeu est d'abord un jeu papier-crayon.
N'hésitez pas à
charger le fichier "Jeu_opérations_ImprA4.pdf" {alternativement, clic sur la
vignette ci-contre à droite.}. Vous trouverez sur la première page du
fichier deux plateaux de jeu à imprimer puis plastifier et sur la
seconde page six feuilles de marque, à photocopier en nombre. Reste
à présenter le jeu aux élèves. |
 |
|
|
 |
J'ai conçu à cet effet un
fichier oOo de type Draw : "Jeu_opérations(v2).odg".
N'hésitez pas à le
charger. Je suppose que vous disposez d'un vidéoprojecteur. Vous
afficherez ainsi un plateau de jeu sur lequel vous déplacerez un jeton
virtuel. Un système de marque permet d'enregistrer les déclarations
successives des deux joueurs. Le dispositif n'est pas des plus
commodes, mais peut tout de même vous être utile. N'hésitez pas à
consulter "Aide_Jeu_Op(v2).pdf". |

|
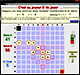
Mais il existe une troisième voie :
confier à l'ordinateur le contrôle du jeu.
Pour un pâle écho de cette solution
cliquez sur l?icône ci-contre à droite.
Si cette copie d'écran vous semble présager de quelque chose de
profitable, et si vous disposez d'un PC sous Windows, chargez mon petit
programme Jeu3Ope.exe en
cliquant sur la vignette ci-dessous à gauche.
|
 |
 |
{Comme beaucoup de mes petites
productions, il n'y a pas d'installation à faire.} J'ai
introduit dans cette version électronique une légère variante.
On ne déplace plus un jeton, mais on désigne une case, parmi les cases
jouables (sous le contrôle du programme) avec la restriction suivante :
on ne peut pas désigner une case déjà jouée. Le joueur doit ensuite
donner le résultat du calcul demandé parmi une liste de possibles. |
A l'usage, on assiste à deux types de
comportement : au début, le joueur a tendance à désigner une
case puis à chercher dans la liste des réponses possibles la bonne
réponse ; puis le joueur devient plus audacieux en cherchant dans la
liste le plus fort résultat (en vue de scorer au maximum) pour désigner
dans un second temps une case compatible avec ce résultat. |
| Les jeux ne sont pas toujours des jeux à deux |
 |
|
 |
Les
jeux présentés jusqu'à présent opposent toujours deux adversaires. Mais
ce n'est pas une nécessité. D'une part, on trouve des jeux solitaires
comme ceux proposés sur ma page Jeux de Calcul.
Mais d'autre part, on trouve aussi des jeux d'équipe tels les deux jeux
présentés maintenant. Ces deux jeux sont très anciens. Ils ont été
présentés par l'APMEP en 1980. |
 |
Concertum (CE/CM) Jeu
par équipes de 3
Plusieurs équipes de
3 joueurs s'affrontent sous la conduite d'un meneur de jeu. Chaque
joueur dispose d'une batterie de 10 cartons numérotés de 0 à 9, ou
d'une ardoise sur laquelle il transcrit un nombre-chiffre. |
|
|
Le meneur de jeu
énonce un nombre entier compris entre 0 et 27. Le but de chaque équipe
est de pouvoir lever au signal 3 cartons (ou équivalents) dont la somme
des nombres inscrits est égale à l'entier formulé. Vous trouverez en base de page 4 de ma brochure
Atelier_DB ... pdf une présentation complète
de ce jeu.
Ce jeu a inspiré de nombreux
auteurs, au point de le transformer en une situation classique
d'étayage ou de validation. Vous
en trouverez un exemple frappant mais intéressant sur cette page :
http://www.ac-grenoble.fr/ien.bourgoin1/spip.php?article642
. |
|
Le jeu est assez ouvert
pour permettre au moins deux stratégies.
La première stratégie est de type
soustractive : les trois membres de l'équipe s'ordonnent d'un
premier jusqu'à un troisième. Le premier joueur choisit le plus grand
nombre-chiffre qui soit inférieur ou égal au nombre proposé. Le second
effectue la soustraction du nombre proposé et du nombre proposé par le
premier joueur ; il en déduit le nombre-chiffre à jouer. le trosième
joueur opère de la même façon. Exemples : 27 = 9 + 9 + 9 ;
24 = 9 + 9 + 6 ; 18 = 9 + 9 + 0 ; 16 = 9 + 7 + 0 ; 8 = 8 + 0 + 0 ; etc.
On note deux pivots pour les calculs : 18 et 9. On doit aussi repérer
la dissymétrie de la charge de calcul de chacun des joueurs et c'est
sans doute le premier joueur qui a la charge la plus faible.
Le modèle sousjacent reste
la recherche du plus fort multiple de 9 inférieur au nombre énoncé par
le meneur de jeu et son écart à ce nombre, mais ce modèle n'apparaitra
pas.
Le seconde stratégie
est de type divisive : dans la division par 3 d'un entier n, on
tient la relation n = 3 x P + R avec 0<= R < 3. On peut repérer :
27 = 3 x 9 + 0, 26 =
3 x 8 + 2, 25 = 3 x 8 +
1, 24 = 3 x 8 + 0, 23 = 3 x 7 + 2 ...
D'où une stratégie : les joueurs de l'équipe s'ordonnent (le premier,
le second, le dernier). A l'énoncé de la valeur à atteindre, chaque
joueur calcule son quotient par 3. Le dernier joueur peut déjà préparer
son carton ou son ardoise. Les deux autres analysent le reste dans la
division (éventuellement vu comme écart). Si ce reste est nul, les deux
joueurs préparent leurs cartons ou leurs ardoises (avec le quotient
déjà calculé). Sinon, le premier joueur ajoute 1 au quotient et prépare
son carton. Le second joueur doit faire attention : si le reste vaut 1,
il prépare son carton ou son ardoise (quotient exprimé), sinon il
ajoute 1 au quotient et
prépare son carton.
Exemples :
26 = (8 + 1) + (8 + 1) + 8 ; 25 = (8 + 1) + 8 + 8 ; 24 = 8 + 8 +
8 ; 13 = (4 + 1) + 4 + 4 ; 11 = (3 + 1) + (3 + 1) + 3. |
 |
Les 6 coups
(CE/CM) Jeu à 2, 3 ou 4 Vous trouverez en base de la page 4 de ma brochure
Atelier_DB ... pdf une présentation de
ce jeu dû à R. Jegou (Ecole Libératrice n°9 - novembre 1980). Pour
chaque partie, la table de jeu doit disposer d'un dé et d'une feuille
de marquage sur le modèle ci-contre (ajouter des colonnes selon le
nombre de joueurs). Chaque joueur lance le dé à tour de rôle. |
 |
|
|
Il inscrit alors dans une case libre
de sa colonne le produit de l'entête de la ligne visée par la valeur du
dé. Les adversaires contrôlent l'inscription. Quand les six cases de
chaque colonne sont remplies, chaque joueur somme le contenu des cases.
Le gagnant est celui qui obtient le total le plus élevé.
Cette situation a le mérite de montrer qu'un jeu peut se pratiquer à
plusieurs, mais justement : s'agit-il vraiment d'un jeu ? |
| Un jeu n'est pas figé |
 |
|
 |
De nombreux jeux, à finalité
mathématique, sont susceptibles de réglages, grâce à ce que les
didacticiens appelleront des variables ... didactiques. Et le loup ici sort de la forêt : Qui
dit variable didactique dit intention didactique ; exit le jeu
finalement ! ou ?
En voici un exemple, déjà présenté sur ma page Jeux de Calcul. |
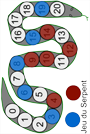 |
Jeu du Serpent (CP/CM) 2
joueurs. Ce jeu,
d?origine allemande, a été présenté par Josiane Helayel dans le n°59 de la revue Grand
N pages 19 à 22 (1996-1997). Ce jeu est de facto très facile à
adapter et couvre les cycles 2 et 3.
Cliquez sur la vignette ci-contre à droite pour consulter un mode
d'emploi complet.
Cliquez sur la vignette ci-contre à gauche pour charger un plateau de
jeu prêt à imprimer.
Pour une monstration en classe, avec vidéoprojecteur, vous pouvez tirer
avantage de mon fichier Libre Office Draw "Jeu_serpent.odg". |
 |
|
|
Puisez dans la pioche
soit un jeton bleu, soit un jeton rouge et amenez-le en bonne position.
Notez que ces jetons sont translucides. Vous aurez cependant à gérer
tous les autres aspects du jeu : tirages aléatoires, calculs
intermédiaires, enregistrement de la suite de coups sur tout support
approprié.
Pour explorer l'ensemble des
possibles de ce jeu, rendez vous sur la page de la Mission Mathématiques Martinique.
Vous y trouverez des plateaux de jeu adaptés à chaque niveau de classe
ainsi qu'un diaporama complet. Une visite s'impose ! |
| Certains jeux sont susceptibles de transfert |
 |
|
 |
Deux histoires d'empoisonement qui
tournent, de façon plus ou moins masquée autour de la notion de
division euclidiene ! |
 |
Le
Pion Empoisonné (CE2/CM1) 2 joueurs Le principe de ce jeu pour 2 joueurs
est simple : on dépose sur la table un certain nombre de
jetons, puis à tour de rôle chaque joueur prélève 1, 2 ou 3 jetons.
Celui qui prend le dernier jeton a perdu. |
 |
|
|
Vous
trouverez ci-contre une version électronique de ce jeu.
Pour un aperçu (bien rapide) de l'implémentation, cliquez sur la
vignette ci-dessus et à droite.
Si le jeu semble vous convenir, téléchargez sur votre PC la version
complète (clic sur l?icône de l'archive LPE.zip ci-contre à droite).
Le logiciel permet à
deux joueurs de s'affronter, l'un d'eux pouvant être l'ordinateur.
Vous trouverez une description complète du jeu électronique dans le
fichier d'aide, dont l?icône apparaît ci-dessous à gauche. |
 |
 |
Ce
jeu est un jeu de prise. Il appartient à la classe des jeux de
Nim. C'est en fait un jeu de Nim à un seul tas. Pour cette notion voir
http://fr.wikipedia.org/wiki/Jeux_de_Nim par exemple.
Il existe donc une stratégie
gagnante s'appuyant sur la notion de position gagnante. Si on appelle Empan le nombre maximum de
jetons préhensibles plus un, alors on est sûr de gagner si on
laisse à l'adversaire Empan
jetons à prendre (compte non tenu du pion empoisonné) et plus
généralement n fois Empan
jetons. |
Ce jeu ne peut pas ne pas
faire penser à la célèbre "course à 20"
de Brousseau. puisque tous deux s?appuient sur le modèle de la division
euclidienne. Vous trouverez un développement un peu plus ample de ce
repérage dans le fichier Aide_LPE.pdf. |
 |
La Gaufre Empoisonnée
(CM) 2 joueurs
Ce jeu a été présenté par l'APMEP en 2005 dans sa brochure "Jeux 7". |
|
|
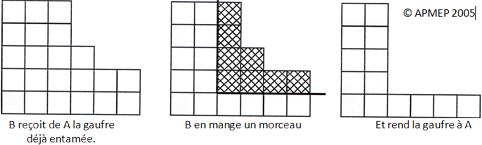
Le principe du jeu est assez simple : Au départ, la
gaufre est représentée par un quadrillage à n lignes et p colonnes.
Chaque carré est un morceau de gaufre, mais le morceau en bas à gauche
est empoisonné. Mordre la gaufre consiste à choisir un morceau,
l'enlever, et avec lui tout ce qui se trouve au dessus et à droite. Les
joueurs mordent alternativement. Celui qui est obligé de mordre le
morceau empoisonné a perdu. A titre d'illustration, voici une phase de
jeu :
|
|
 |
 |
Mais voici un autre jeu, a priori
bien différent : Le jeu des diviseurs
(APM) (CM) 2 joueurs Un nombre N est choisi et la liste de
ses diviseurs est dressée, incluant N mais pas 1. Par exemple si on
choisit 72, alors on dresse la liste "2 ; 3 ; 4 ; 6 ; 8 ; 9 ; 12
; 18 ; 24 ; 36 ; 72". Le
premier joueur choisit un diviseur de N et l'enlève avec tous ses
multiples. Par exemple, si le joueur A choisit 12 ; il enlève 12
; 24 ; 36 ; 72 et il ne restera plus que 2 ; 3 ; 4 ; 6 : 8 ; 9 ; 18.
Le second joueur choisit
alors un diviseur restant et l'enlève avec tous ses multiples. Par
exemple, si le joueur B choisit 4 ; il enlève 4 ; 8, laissant 2 ; 3 ; 6
; 9 ; 18. Et ainsi de suite. Le joueur qui ne peut plus jouer a
perdu.
Une variante est la suivante
: on injecte 1 dans la liste initiale et le joueur qui choisit ce
nombre a perdu. Le 1 joue donc le rôle de la case empoisonnée du jeu de
la gaufre.
Voici
le point important : si on choisit pour nombre N un
entier n'ayant que deux diviseurs premiers (ex: 72 = 2^3x3^2),
alors ce jeu est équivalent au jeu de la gaufre empoisonnée. Vous en
trouverez l'explication à la page 147 de la revue "Jeux 7" de l'APMEP
-déjà citée ci-dessus. Le
repérage de cet isomorphisme entre ces deux jeux suppose une
mathématisation sans doute hors programme du cycle 3. Mais elle ne
laisse pas d'interroger sur la nature profonde d'un jeu. Cette question
avait déjà surgi lors de la présentation du jeu du Quinze-Vainc
... |
 |
Retour
au jeu de la Gaufre empoisonnée.
Le jeu de la gaufre empoisonnée est
aussi un jeu de Nim. Il existe donc une stratégie gagnante.
Elle est même ici particulièrement brutale ! Le premier joueur mange
presque toute la gaufre, ne laissant que la colonne la plus à gauche et
la ligne la plu basse. Puis il réplique systématiquement au second
joueur en jouant comme lui mais symétriquement (par exemple si le
second joueur mange 4 cases de la ligne inférieure, alors le premier
joueur mange 4 cases de la colonne la plus à gauche).
La connaissance de cette stratégie gagnante assure au joueur qui
commence un gain rapide de la partie, tuant l'intérêt du jeu.
D'où l'idée de faire évoluer le
jeu. On peut par exemple rajouter une contrainte quant à la taille de
la prise.
 |
La
contrainte peut être statique (pas plus de tant de cases à la fois) ou
dynamique (pas plus de telle fraction des cases restantes). Mais
qui dit contrainte dit risque de transgression, qui doit être détectée
et, éventuellement, sanctionnée !
Ici encore, l'apport de
l'informatique est évident.
J'ai donc programmé un démonstrateur permettant à deux joueurs (ou deux
équipes) de s'affronter. |
 |
L'ordinateur ne joue pas et se contente
d'orchestrer les phases de jeu et d'en vérifier la régularité. |
|
 |
Pour une présentation complète du
démonstrateur, cliquez sur la vignette ci-dessus à gauche. Pour jauger rapidement de l?apparence
de ce démonstrateur, cliquez sur la vignette ci-contre à gauche.Si le jeu vous convient, téléchargez
sur votre PC la version complète en cliquant sur l?icône de mon
logiciel (juste au dessus mais à droite). |
Si vous tester mon logiciel, essayer de
(faire) jouer avec les divers réglages proposés pour noter comment
ceux-ci influent sur la nature même du jeu en lui conférant une
dimension calculatoire plus ou moins importante.
Vient la question : si
l'objectif est de scorer,
n'est-il pas antinomique de celui de ne pas manger la dernière case ?
Une autre façon de
faire évoluer le jeu consiste à limiter la façon de croquer la gaufre.
On peut ainsi décider qu'il n'est
possible de croquer 1/ que dans le prolongement horizontal ou vertical
de ce qui a été mangé ; ou 2/ qu'à condition d'ébarber autant de lignes
que de colonnes.
Ce jeu devient équivalent, quoiqu'en négatif, du jeu du Dornim. Ce jeu est lui-même équivalent au jeu
des deux tas d'or. Pour une découverte de ces jeux très classiques,
cliquez sur la vignette ci-contre à droite. |
 |
Pour jouer au jeu des deux
tas d'or , il convient juste de se constituer deux tas : des haricots
secs, rouges et blancs, suffisent.

|
Pour jouer au jeu du Dornim, il faut
disposer d'un plateau de jeu. Comme il ne s'agit que d'un quadrillage,
on peut choisir de le faire tracer par les élèves.
Vous trouverez peut-être plus commode d'imprimer puis de plastifier un
plateau tout prêt. En cliquant sur l'icône ci-contre à droite, vous
téléchargerez une feuille A4 qu'il ne vous restera plus qu'à imprimer.
Si vous utilisez ces plateaux, je vous recommande d'utiliser les jetons
proposés sur ma page Jeux
de Calcul .
|
|
Fidèle à mes habitudes, je
vous propose la version informatique du plateau de jeu. Il s'agit
encore une fois d'un embryon de simulateur qui nécessite Libre Office !
Je n'insiste pas ...
Cliquez sur la vignette ci-dessus à gauche pour charger ce fichier.
|
| Les jeux de Didier Faradji |
 |
|
 |
On ne présente plus
ces trois jeux : "Decadex Magix34 Multiplay" imaginés par D.
Faradji dans les années 2000 et diffusés par le CRDP de Franche-Comté
avec l'appui de la Cité des Sciences et de l?Industrie.
 |
Vous
pouvez acheter ces trois jeux en vous rendant à cette adresse : http://jeux-mathematiques.fr/index.php?id=multiplay
Vous trouverez sur le site de Publimaths une fiche de description rapide.
Cette fiche résume assez drastiquement la prière d'insérer de la
brochure APMEP n° 606. |
Pour vous faire une bonne idée des
intentions de l'auteur, le plus simple consiste à lire le livret
pédagogique d'accompagnement ...
A cet effet cliquez sur la vignette ci-contre à gauche : vous chargerez
ce livret d'une trentaine de pages au format PDF.
Mais il vous faut
aussi lancer quelques parties. C'est ici qu'entre en scène mon
simulateur (3,3 Mo). Commencez par charger le programme en
cliquant sur la vignette ci-contre à gauche. |
 |
|
 |
| Comme toutes les
propositions de cette page, il n'y a pas d'installation à faire.
Contentez-vous de déposer le fichier dans un endroit accessible.
Pour avoir un aperçu des
fonctionnalités du logiciel, ouvrez le fichier DM34Xplay.pdf
(clic ci-contre à droite). |
 |
 |
Mon travail se veut une aide, soit pour
vous permettre de découvrir le potentiel des jeux inventés par D.
Faradji, soit pour faciliter la présentation que vous en ferez à votre
classe. Il n'est donc pas
question que vous substituiez au coffret mon logiciel. |
|
|
Je vous remercie de
respecter cette clause de copyright. |
|
|
|
|