Calcul

Bribes de cours

Le contenu de cette page reprend et développe certains éléments d'un cours magistral tenu devant des étudiants de M1, dans le cadre de leur préparation au concours de recrutement du professorat des écoles.

Nous commençons par le contenu du diaporama créé à l'occasion, ainsi que quelques déclinaisons :


Cliquez sur la vignette ci-dessus pour charger le diaporamma du CM. {1,92 Mo à charger}	En cliquant sur la vignette ci-dessus, vous chargez le même contenu, mais avec un thème graphique différent.	En cliquant sur l'une ou l'autre des vignettes ci-dessus, vous chargez un fichier PDF reprenant les diapositives des diaporamma. Utile comme roue de secours si l'ordinateur utilisé ne dispose pas d'une visionneuse Powerpoint récente (> 2003). Peut se révéler commode pour circuler rapidement d'une page à une autre grâce au panneau de navigation 'Pages'. Attention pour le téléchargement : Les fichiers pèsent respectivement 2,5 Mo et 1,8 Mo..	Pour impression uniquement. Permet de lire sur papier A4 les 39 diapositives, regroupées 2 par 2. {Le fichier pèse environ 2Mo.}
Les deux diaporammas présentés ici ont le même contenu. Seul le "thème", pour reprendre la terminologie Microsoft change. Selon le vidéoprojecteur disponible et les conditions d'éclairement, j'opte pour l'une ou l'autre de ces versions.

Les thèmes de mon exposé seront repris et donneront lieu à quelques ouvertures dans les puces à suivre ci-dessous.
Sommaire du diaporamma alias plan du cours.

A1/ Origine du calcul
A2/ Qu'est-ce que le calcul ?
A3/ Règles
A4/ Disponibilités nécessaires
A5/ Flexibilité du calcul
B1/ La trilogie 2002 du calcul à l'école
B2/ La refondation 2008

{Cliquez sur l'un des titres ci-dessus pour accéder directement à la section}

A1/ Origine du calcul

La notion de calcul est très ancienne puisque on en trouve trace en Mésopotamie vers 8 000 ans av. JC et qu'on en a des preuves attestées dès la civilisation Sumérienne vers 3000 ans av. JC.

Ces civilisations voient le développement des premiers échanges -qu'on pourrait appeler commerciaux- il leur faut un dispositif pour mémoriser l'information numérique (combien de têtes de bétail ?) et calculer son évolution.
L'outil principal consistat longtemps en des petits 'cailloux', d'abord naturels, ensuite fabriqués en terre cuite.
Chaque forme représentait un ordre de grandeur : unité, dizaine, centaine, millier, et sans doute myriade. Pour représenter une quantité, on assemblait pour chaque ordre

de grandeur autant de petits cailloux que nécessaire.
Il s'agit donc là d'une numération additive pure, comme celle usitée en Egypte antique.
Avec la fabrication artisanale des représentants de chaque ordre, on tint des figures stéréotypes, prélude à l'invention des chiffres après celle de l'écriture. Au risque d'insister, ces cailloux servirent donc d'outil pour nommer/représenter les nombres et d'outil pour calculer.
Plus près de nous, les Romains héritent des petits cailloux, dont ils oublient la forme car ils les figent sur des dispositifs à coulisse : invention de l'abaque, comme l'exemplaire présenté ci-contre à gauche.
A dire le vrai, le mot latin abacus désignait une plaque sur laquelle des

colonnes étaient gravées, un peu à l'image de nos tableaux de numération décimale ; on disposait ainsi des petits calculi pour affectuer des opérations de diverses natures. Ces tablettes était réalisées le plus souvent en terre cuite mais on en trouvait aussi en pierre ou en albâtre. Ce dispositif perdura très longtemps puisqu'on trouve encore au XVième siècle des tables à calcul, comme celle représentée ci-contre à droite (Musée de Dinkels-Buhl en Allemagne).
Dans le même temps, les romains installaient les petits cailloux sur des tables à fentes, inventant ainsi une des premières machines à calculer de notre zone géographique. On pourra comparer cette machine aux bouliers chinois ou japonais.

On doit à Gerbert d'Aurillac (938-1003) devenu pape sous le nom de Sylvestre II en 999 la diffusion de l'écriture décimale, empruntée aux Indiens et perfectionnée par les Arabes. Notez sur l'illustration ci-contre à gauche la graphie adoptée pour notre 5 : une

sorte de zéro, interdisant pour un temps son invention !
Mais la pénétration de la numération écrite en Europe fut très lente. Le peuple, du plus humble au plus cultivé, continuait à avoir une grande méfiance ou une ignorance totale du calcul écrit. Le calcul érait donc l'apanage d'une petite élite de professionnels partagée entre les algoristes et les abacistes. Les deux écoles se firent la guerre au moins jusqu'au XVI-ième siecle : la querelle des maths modernes fut bien courte en comparaison.
Les abacistes (du mot albâtre), à droite sur l'illustration ci-contre, en tenaient pour "jeter le jeton" quand les algoristes (penser à nos algorithmes de calcul), à gauche, défendaient l'idée de procéder par les seules écritures.
Ce sont ces derniers qui finirent par l'emporter, grâce à la

Révolution Française qui vit interdire le recours à l'abaque, que ce soit dans les écoles publiques ou les administrations.
Deux éléments ont du peser lourd dans la balance : les algoristes n'avaient pas besoin de matériel, leur méthode pouvait être mise en œuvre par tout le monde à condition d'apprendre le calcul posé (déjà l'antienne sinon de la démocratisation du moins de la scolarisation) et, par ailleurs, cette méthode laissait des traces, permettant de s'interrompre et, peut-être plus sûrement, de contrôler ses calculs, donc de débusquer d'éventuelles erreurs.

Voir sous l'onglet [Opérations] une discussion sur les qualités attendues d'un "bon" algorithme de calcul.
Bien entendu, si l'irruption du calcul posé prit tant de temps c'est certainement du fait de l'absence d'un système de numération performant, tant dans sa logique que de son écriture. Il fallut ainsi attendre que la numération décimale de position soit suffisament bien formalisée, ce qui sera le cas avec Simon Stevin (Flandres 1548-1620) qui invente, à peu de choses près, l'écriture virgulaire des fractions décimales, rendant possible du même coup la généralisation des algorithmes de calcul des nombres entiers aux nombres décimaux.

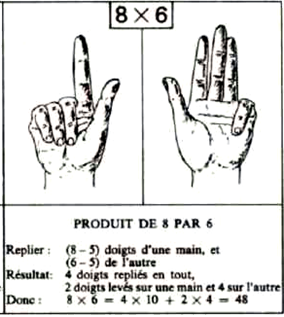
On tient comme acquis, qu'à défaut de maîtrise du calcul écrit, les hommes avaient très tôt mis en place un système efficace de calcul : le calcul digital.
Ce type de calcul est attesté depuis les temps reculés, et l'on sait que les Incas se sont appuyés sur leurs 20 doigts, pour mettre en place -parmi les premiers- un système de numération de position (presque régulier) et un système de nomination

de leur vingt chiffres à partir du nom de leurs membres. L'imprégnation du shéma corporel sur les chiffres romains ( le V n'étant rien qu'un condensat de la main, 1 pouce et 4 phalanges soudées) est à peu près certaine.
On invoquera aussi facilement nos habitudes de comptage avec la main, encore au XXI-ième siècle..
D'une certaine façon, la main fut sans doute l'une des plus anciennes machines de calcul que l'homme ait enventé. On en peut en faire une lecture moderne (inspirée de l'informatique) : nos doigts tiennent lieu de registre d'affichage (je montre 7), de registre-mémoire (et je retiens 2), de registre calcul (et j'ajoute 3).

C'est que, de tous temps, la mémoire de l'homme est fragile et le risque de surcharge cognitive toujours possible. D'où la recherche de substituts efficaces au seul travail du cerveau. {Voir l'onglet [Calcul mental et réfléchi].}

Les règles de Néper en sont un autre exemple : du XVI-ième au XIX-ième siècle, on pouvait acheter des boites -de la taille d'une grosse boîte d'allumettes- contenant onze baguettes. Elles permettaient le calcul de multiplications d'une taille assez conséquente, sans avoir à mobiliser ses tables de multiplication, puisque par le jeu des baguettes adroitement posées, il suffisait de cumuler des résultats partiels.
On pouvait même calculer des racines carrées -à condition de maîtriser l'algorithme !

Un dernier écueil mérite d'être souligné : jusqu'à la Révolution Française, les unités de mesure étaient très variables, d'une région à l'autre d'une part, en général non décimalisées d'autre part. Ainsi une Livre valait 20 Sols à peu près partout, mais 1 sol valait 15 Deniers à Paris et 12 à Tours ; en revanche on tenanit partout les équivalences 1 Liard = 3 Deniers, 1 Denier = 2 Oboles, 1 Pistole = 10 Livres.
Je vous laisse calculer la part d'héritage de 3 garçons au décès de leur père, sachant qu'il leur léguait 25 Pistoles, 4 Deniers et 10 Sols et que l'aîné devait emporter la moitié de l'héritage contre le cinquième pour le cadet...
{Ci-contre Poids de marc de Charlemagne. Cf. Wikipédia.}

En résumé : 1/ le mot calcul trouve son origine dans le mot latin calculus/calculi qui désignait un/des petit/s caillou/x. {C'est aussi pour
cela que nos reins sont susceptibles de souffrir de calculs dit rénaux.}
2/ faute de système de notation efficace, l'homme inventa très tôt des machines pour faciliter ses calculs. Il n'est donc
pas étonnant que les calculettes (des téléphones notamment) aient été adoptées si rapidement.
3/ ce n'est qu'à la Révolution Française que l'on voit une convergence du système d'écriture décimal et d'un système
d'unités de mesure cohérent et régulier. L'essor des machines de calcul est alors incontournable.
Pour aller plus loin
A défaut de présenter une bibliographie, beaucoup trop vaste, j'indique quelques adresses de site qui m'ont semblées mériter la visite.

Sur l'histoire des nombres et du calcul : http://www.math93.com/histoire-nombres.htm
http://serge.mehl.free.fr/chrono/Gerbert.html
http://promenadesmaths.free.fr/histoire_arithmetique.htm
Sur la querelle des albacistes et des algoristes :
http://www.encyclopedie-universelle.com/abaque-calcul9-renaissance-XIXeme.html
Sur l'histoire des instruments et machines à calculer ainsi que sur leur analyse :
http://www.math.ens.fr/culturemath/materiaux/poissard/fiche1.pdf http://www.math.ens.fr/culturemath/materiaux/poissard/fiche4.pdf (histoire des bâtons de Neper) http://nathalierun.net/passions/boulier/histoire.htm (Une présentation du/des boulier/s parmi tant d'autres)
Sur l'histoire des unités de mesure :
http://croac.chez-alice.fr/Pensees/Unites.htm
http://passionmedievale.sixieme-cercle.com/donjon/historia/mesure-et-outils.html http://fr.wikipedia.org/wiki/Unit%C3%A9s_de_mesure_anciennes_%28France%29

Vous trouverez sur mon site des explications et des simulateurs des outils de calcul suivants :

Compteur à 4 roues (multi-bases)
Abaques à 4 tiges (multi-bases)
Bandes de Neper (variante des réglettes de Neper)
Boulier chinois. Pour comparer les fonctionnalités de ces machines, cliquez sur la vignette ci-contre à droite pour charger un fichier PDF correspondant. Attention : il s'agit plutôt d'un document pédagogique à projeter en classe ou à photocopier pour le faire remplir à la main par les étudiants. De facto, il est donc verrouillé.

Je clos cette section avec l'image d'un instrument irremplaçable jusque dans les années 1980 : la règle à calcul !

Ne fut définitivement abandonnée par son fabricant qu'en 1990.
Voir une présentation rapide par un club de maths de l'outil "Règle à calculs" ici : http://clgdrouyn.fr/La-regle-a-calcul.html

A2/ Qu'est-ce que le calcul ?

Dans la langue courante, quand il ne s'agit pas d'une affection biliaire ou urinaire, le calcul: désigne -selon Littré- tout type d'opération par laquelle on trouve le résultat de la combinaison de nombres ou de quantités. D'où les locutions "calcul exact", "calcul faux", ou très fréquemment "sauf erreur de calcul". Un résultat est escompté, qui permette de prendre une décision : "de calcul fait" à rapprocher de "tous comptes faits".
Plus largement, le calcul désigne l'ensemble des moyens qu’on combine, des mesures qu’on prépare en vue du succès d’une affaire. Le sens peut devenir négatif voire péjoratif : "Il a agi par calcul", "Il a fait un mauvais calcul.", "Cela n’entre pas dans mes calculs.", "Il a déjoué tous les calculs.".
Le calcul tient alors du stratagème, "il est mûrement pensé", ou de la machination, "un calcul diabolique", comme seul un esprit calculateur peut en mettre au point. On retrouve bien dans toutes ces expressions la défiance populaire à l'égard du calcul perçu comme la science des nombres.

Lorsqu'il s'applique à l'école, le calcul renvoie à l'art de "manier les chiffres". Les futurs bons en maths sont d'abords forts en calcul quand certains de leurs camarades seront toujours mauvais en calcul. Le calcul tiendrait donc de l'art, ou du don.

{Ci-contre, la figure du bon élève : Agnan. Clic sur la vignette pour visiter le site officiel.}

Les adultes évoqueront autrement le calcul à l'école : "Le niveau de calcul a encore baissé …", "Les élèves doivent savoir calculer à l'entrée en sixième …", etc.

Mais le calcul s'apprend parce qu'il s'enseigne, et, souvenir du temps où les candidats à un poste de précepteur ou d'enseignant dans les petites écoles rurales circulaient porteurs d'un chapeau avec une, deux ou trois plumes, selon le degré de ses compétences (il
pouvait savoir enseigner la lecture, la lecture et l’écriture ou la lecture, l’écriture et le calcul), dans toute école on doit apprendre le français, l'histoire et le calcul.Pas un ministre de l'Education d'oublier de rappeler cet adage lors de sa prise de fonction !
Sur l'histoire du chapeau à plumes, voir sur le site de lyon-2. Un livre portant sur ce thème avait été publié en 2002 puis 2007 : Les carnets d'un maître d'école autrefois. Trois plumes au chapeau par Clément Brun chez Fontaine de Siloé éditeur, ISBN 2-84206-192-6. Il est malheureusement devenu indisponible.}
Fermons ce paragraphe dévolu à la recherche du sens courant du mot calcul en remarquant le poids de ce petit mot dans l'inconscient collectif.

Il est beaucoup plus difficile de donner une définition acceptable par la communauté des mathématiciens du mot calcul.

Osons cependant :

En mathématique, un calcul est une combinaison d’objets mathématiques (représentés par des symboles) obtenue grâce à des opérations, selon des règles précises, afin d’obtenir un résultat.
Exemples : calcul algébrique, barycentrique, vectoriel, tensoriel, différentiel, intégral, propositionnel, formel, trigonométrique, matriciel, exponentiel, booléen, statistique, binaire, numérique approché ou non ...

Les objets sont pour nous, candidat(e)s au CRPE, les nombres -entiers, décimaux, rationnels, réels- qu'ils soient exprimés sous formed'une valeur ou d'une expression littérale.
Les opérations sont les opérations classiques : addition (et soustraction), multiplication. On y ajoute improprement la division. Voir sur ce point sous l'onglet [Opérations].
L'art du mathématicien est de savoir utiliser le calcul approprié à un instant donné, quitte à changer de cadre lorsque cela est nécessaire. J'en donne des exemples à la section A5.

Pour nous, candidat(e)s au CRPE, le calcul est essentiellement numérique, mais il peut recouvrir trois formes.

Forme algébrique comme dans :
ou dans :
Forme arithmétique comme dans :	3 Shadocks pompent 3 litres en 3 heures. Combien de litres 30 Shadocks pomperont-ils en 30 heures ?
Forme classique comme dans :	C'est les soldes ! Un prix passe de 35 € à 33 € … Valeur relative de la baisse (en %)

Dans le dernier cas, le calcul pourra être exact ou approché.

Pour être bien conduit, le calcul suppose un certain nombre de connaissances et de capacités.

¤ Compréhension de notre système de numération décimale de position :

valeur des chiffres selon leur position
conversion 10 pour 1

notamment pour la maîtrise d'algorithmes efficaces (gestion des retenues, règle des zéros ...)
¤ Compréhension qu'une valeur peut être exprimée de plusieurs façons :

canoniques :	45 16 2/7 0,2 3,57.10⁶ 8,23.10^-8
non canoniques :	3x15 4² 22/77 7/35 0,357E7 0,823N7

¤ Maîtrise des règles de transformation :

propriétés, syntaxe des opérations Cf. section A3

¤ Nécessaire disponibilité de répertoires :

tables, formules, coups de main Cf. section A4

¤ Grande flexibilité, c'est-à-dire la possibilité de changer de cadre Cf. section A5

A3/ Règles

Dans ce qui suit les symboles représentent aussi bien des nombres que des variables.
Les écritures sont censées valides pour les nombres mis en jeu.

Vous pouvez charger un récapitulatif facile à imprimer (recto-verso en A4) en cliquant sur la vignette ci-contre à droite.

Pour vous entraîner, rendez-vous, par exemple, sur ma page CRPE 2010. Vous y trouverez une brochure intitulée 'Soutien numérique' proposant page 7 divers calculs numériques.

On calcule avec deux opérations : + (-) et × Pour une étude plus précise, glisser sous l'onglet [Opérations].

Ces deux opérations sont commutatives :
    a + b = b + a   a × b = b × a
Elles sont aussi associatives :
    a + (b + c) = (a + b) + c    a × (b × c) = (a × b) × c
L'une est distributive par rapport à l'autre :
       a × (b + c) = a × b + a × c
Illustrations :

1 + 2 + 3 + 4 + 5 = 1 + 4 + 2 + 3 + 5 = 3 x 5 = 15
14 x 15 = 7 x 2 x 3 x 5 = 3 x 7 x 2 x 5 = 21 x 10 = 210
51 × 15 = 50 × (10 + 5) + 15 = 500 + 250 + 15 = 765

On peut donc simplifier :

Expression1 + k = Expression2 + k <=> Expression1 = Expression2
k × Expression1 = k × Expression2 et k non nul <=> Expression1 = Expression2

Les opérations sont compatibles avec la relation d'ordre :

a < b => a + c < b + c et de même si les inégalités sont au sens large.
Mais attention :
a < b et c > 0 => a.c < b.c et de même si les inégalités sont au sens large.
a < b et c < 0 => a.c > b.c et de même si les inégalités sont au sens large.
Attention encore, quand on élève au carré :
a < b => a² < b² et de même si les inégalités sont au sens large.
Mais : a² < b² => |a| < |b| et de même si les inégalités sont au sens large.

Gestion des écritures multiplicatives

Définitions : aⁿ = a × … × a {n termes} a^1/n = b <=> bⁿ = a a^-n = 1/aⁿ = (1/a)ⁿ a^1/2 = √a
En particulier, la racine d'un produit de nombres positifs est le produit des racines de ces nombres. Idem pour un quotient.
Propriétés : a^p × a^q = a^{(p + q)} a^p / a^q = a^{(p - q)} (a^p)^q = a^{(p
× q)}

aⁿ × bⁿ = (a.b)ⁿ aⁿ / bⁿ = (a/b)ⁿ

Mais attention (a + b)ⁿ n'a jamais été égal à aⁿ + bⁿ ! Pour s'en souvenir, penser aux identités remarquables.

Simplification des écritures fractionnaires

a/b × c/d = ac / bd et a/b ÷ c/d = a/b × d/c = ad / bc en sorte que (k.P)/(k.Q) = P/Q.
Cas des échafaudages : Attention aux expressions ambigües. Ainsi, une expression a/b/c peut être considérée comme la fraction a/b divisée par le nombre c ou comme le nombre a divisé par la fraction b/c.
Dans le premier cas on obtient la fraction a/bc, dans le second la fraction ac/b.
Testez avec l'écriture 3/4/5. Selon votre interprétation, vous trouverez 0,15 ou 3.75 ...

Dénominateur commun

a/b + c/d = (ad + bc)/bd et a/b - c/d = ((ad - bc)/bd Voir conseil méthodo n°2.
Attention : la fraction (a + b)/(c + d) ne se laisse pas décomposer en la somme de a/c et de b/d en général ...

A4/ Disponibilités nécessaires

Un bon calculateur, qu'il s'agisse d'un calcul mental, réfléchi ou instrumenté, connait ses tables d'addition et de multiplication.

Les tables sont sues (sous la forme Table de Pythagore) au moins jusqu'à 15 + 15 et 12 × 12.
Il sait circuler parmi les tables qu'il structure autour des deux diagonales :

¤ pour l'addition les nombres qui font 5, 10, 15, 20
et ceux dont l'écart est de 5, 10, 15, 20 ...
¤ pour la multiplication, les carrés parfaits, les produits juste avant, juste après, juste en dessous, juste en dessus ...

Il sait ses doubles, ses presque-doubles, les quintes et sans doute les triples.
Il connait les équivalences 2 × 5 = 10 4 × 25 = 100 8 × 125 = 1 000 et peut-être aussi 16 × 625 = 10 000
{Tous ces points sont développés sous l'onglet [Opérations]}

Un bon candidat connait par ailleurs la table des nombres premiers au moins jusqu'à 37, voire 53. A défaut, il sait la reconstruire rapidement en circulant dans la liste des nombres de la forme 6×k ± 1. Pour mémoire, voici cette liste jusqu'à 150 :

2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149

{Vous trouverez sur ma page ArithRevo.htm un logiciel (PC uniquement) permettant de retrouver cette liste, entre autres.}

Un élève de l"école primaire connait un certain nombre de formules pour calculer des aires et des périmètres simples. Ce formulaire est plus conséquent pour un candidat au CRPE.

Sont à connaître :

les formules donnant le périmètre d'un rectangle ou d'un cercle,

celles donnant l'aire des triangles, rectangles, trapèzes, disques,

celles donnant les volumes des cônes et des cylindres, des parallélipipèdes, éventuellement des sphères.

Cliquez sur l'imagette ci-dessus pour charger un formulaire bien commode (un recto au format A4).
Ce formulaire contient par ailleurs un rappel sur les applications basiques du théorème de Pythagore : longueur de la diagonale d'un carré en fonction du coté et mesure de la hauteur dans un triangle équilatéral.

Le calcul de la hauteur d'une pyramide à base carrée, d'où celui du volume, est assez souvent demandé au concours. Quand toutes les arêtes mesurent a, on doit pouvoir retrouver h = a.(√2)/2 et V = a³(√2)/6.

De nombreux calculs -d'angles ou de temps- obligent à des conversions. La maîtrise des techniques associées est incontournable. Cliquez sur la vignette représentant un rapporteur circulaire ci-contre à droite pour charger un PDF les résumant.

Deux-plus une- identités remarquables (soit trois et seulement trois !) pour le concours. En voici une vision géométrique :

(a + b)² = a² + 2.ab + b²	(a - b)² = a² - 2.ab + b²	(a + b).(a - b) = a² - b²

On calcule mieux (avec moins d'erreurs), plus vite et plus longtemps quand on est méthodique.

Principe méthodo n°1 : Diviser pour mieux régner !
Dans une expression complexe, on isole les termes, quite à les nommer, on les calcule séparément puis on effectue la synthèse de tous ces calculs partiels.
Illustration :

Principe méthodo n°2 : Aller vers le maximum de simplification avant de calculer :

-> On rend irréductibles les fractions, on cherche toujours les plus petits dénominateurs communs (via le ppcm).
Illustration :

-> On chasse systématiquement les carrés de sous les racines.
Illustration :

Principe méthodo n°3 : On factorise quand c'est intéressant :
-> Le principe est plus facile à énoncer qu'à appliquer. Seule l'expérience, donc la pratique, permet d'énoncer quand -et quoi- il faut factoriser. On peut s'en tenir à une règle simple dans un premier temps : "le facteur dit commun doit être commun à tout le monde, pas à un petit bout du calcul".
-> Penser aux expressions conjuguées !
Rappel :

Illustration : Expressions conjuguées (exemple)

Entrainez-vous : analysez la figure ci-contre à droite et retrouvez le fait que le rectangle bleu est proportionnel au rectangle rouge .

Principe méthodo n°4 : On oublie la calculette !
-> On calcule formellement l'expression en jeu jusqu'à obtenir une expression incompressible. La valeur obtenue est appelée une valeur exacte.
-> On ne calcule une valeur approchée, qu'à la toute fin de son calcul,

¤ parce que l'on veut vérifier la plausibilité de la valeur exacte,
¤ parce que le calcul correspond à une longueur mesurable sur un tracé (éventuellement à l'échelle) et que l'on veut vérifier la qualité du tracé,
¤ parce que c'est demandé.

-> Dans un calcul à tiroir, on réutilise la dernière valeur exacte dans le calcul à venir, jamais sa valeur approchée.
Entrainez-vous : analysez la figure ci-dessous et calculez l'aire du triangle équilatéral.

Eléments de solution : Soit a la longueur du côté du triangle équilatéral. On sait calculer la hauteur : h = a * Rac(3) / 2 où Rac désigne la racine carrée. L'aire vaut donc A = a² * Rac(3) / 4. Maintenant : Observez bien les demi-cercles posés à la base ; celle-ci mesure 1 + Rac(5), où Rac(5) désigne la racine carrée de 5. On calcule le carré, soit a² = 2 * (3 + Rac(5)) et on en déduit la valeur exacte de l'aire : A = (3 + Rac(5)) * Rac(3) / 2. Valeur approchée : Avec une calculette simple, on trouve la valeur de 4,534567884. On arrondit avec bon sens. Ainsi, si l'unité était le centimètre, une précision linéaire au mm semble acceptable, d'où une précision au mm² ; une valeur acceptable de l'aire en cm² est 4,5346 ( on a arrondi au mm² supérieur).

A5/ Flexibilité du calcul

Principe méthodo n°5 : Il y a toujours plusieurs façons de s'y prendre. En général, l'une des méthodes se révèle plus efficace !
Voici quatre illustrations de ce principe :

	Exemple 1 : Dans un triangle rectangle de côtés mesurant respectivement 40 et 30 unités, on voudrait connaitre la hauteur relative à l'hypothénuse. Méthode brutale : on installe deux inconnues supplémentaires, "x" et "y" comme sur le shéma ci-contre, puis on tricote : (a) (x + y)² = 30² + 40² ; (b) x² + h² = 40² ; (c) y² + h² = 30². Surtout ne pas effectuer un quelconque calcul à ce point. On reconnait dans le terme droite de (a) une expression archimédienne : 3² + 4² = 5² (à connaitre par cœur). D'où : 30² + 40² = 502 soit (d) x + y = 50 !. Par soustraction terme à terme des relations (b) et (c) on obtient : (d) x² - y² = 40² - 30² ; on reconnait là une identité remarquable - 2 fois ! (x + y)(x - y) = (40 + 30)(40 - 30) = 700. Compte-tenu de (d), on peut proposer : (e) x - y = 700 / 50 = 14. A ce point du calcul, on tient un système -simple- de deux équations linéaires en x et y. La résolution n'est pas difficile et on trouve : x = 32, y = 18. Ne reste plus qu'à reporter dans (b) ou (c) pour exhiber h² = 8² * 3², d'où -enfin- h = 8 * 3 = 24. La méthode brutale est, ici, algébrique, mais une méthode algébrique n'est pas toujours brutale ... Méthode raffinée : on change de cadre (au sens didactique). On calcule l'aire de deux façons différentes. D'où : 50 * h = 30 * 40 => h = 3 * 4 * 100 / 50 = 24. La méthode raffinée s'appuie sur la théorie de la mesure ici. Mais ce n'est pas toujours le cas : nombre de calculs d'aires manquent de raffinement.
	Exemple 2 : On demande de calculer la valeur d'une expression algébrique A comprenant 2 racines carrées. Méthode brutale : on élève l'expression au carré et on se dépatouille (ça marche plus souvent qu'on ne croit). Ici : A² = 153 + 2 Rac (153 * 68) + 68. Mais voilà la bonne surprise : 153 * 68 = 10404 = 102² ! Il n'est pas difficile de conclure : A² = 153 + 68 + 2102 = 425. Ajoutons un peu de douceur à ce calcul brut : 400 = 4100 = 4425, Donc 425 = 1725. Nous tenons notre résultat : A = 5Rac(17). Méthode douce : on commence par analyser les deux facteurs, à la recherche des carrés cachés. Il vient facilement : 153 = 917 => Rac(153) = 3Rac(17) et 68 = 4Rac(17) => Rac(68) = 2Rac(17). On retrouve, mais bien plus vite, le résultat énoncé précédemment.
	Exemple 3 : On demande de calculer la valeur de l'expression présentée ci-contre à gauche. Dans un autre temps, c'eut été une punition, pour un mauvais drôle collé le dimanche. Mais ce temps est révolu ! L'on anticipe un échafaudage impossible. Seule solution : rendre dynamique sa lecture en interprétant l'expression fournie comme le dernier état d'une suite de transformations successives, à partir d'une valeur très simple. Nous changeons donc d'outil et appelons au secours les fonctions numériques, et surtout ici, la possibilité de les composer ! Et d'invoquer la fonction x -> f(x) = 1 + 1/x. Il suffit de réitérer cette fonction 8 fois de suite à partir de la valeur 3. La démarche est peut-être un peu plus longue, mais assurée. Il vient : 3 -> 4/3 -> 7/4 -> 11/7 -> 18/11 -> 29/18 -> 47/29 -> 76/47 -> 125/76. Noter qu'il n'est pas difficile de traiter ce genre de calcul avec un tableur ! Cliquez sur l'imagette ci-contre pour faire apparaître une copie d'écran d'un traitement avec Excel. La copie d'écran fournit les indications nécessaires pour reproduire la démarche avec n'importe quel tableur. On peut prolonger la table vers le bas. Pour une explicitation de ce qui se passe, se reporter -parmi tant de pages disponibles sur le sujet- au site de jc.michel@gecif.net .
	Exemple 4 : On demande de calculer l'expression : 1 + 2 + 3 + 4 + … + 8 + 9. Pas de problèle se dit-on ! Il suffit de sommer progressivement ; on fait comme on a dit et on trouve 45. Mais maintenant on demande de calculer : 1 + 2 + 3 + … + 49 + 50 +… + 99. On repère que l'on peut remembrer pour ajouter 1 à 99, 2 à 98, etc. jusqu'à 49 à 51. Mais que fait-on du 50 au centre ? On suspecte vite que l'on doit trouver quelque chose qui permette de calculer rapidement la somme de n entiers consécutifs à partir de 1. Et si on doublait l'écriture mais en inversant la recopie de la seconde ligne ? Chaque terme de la somme serait marié avec un autre terme de la somme, y compris ce pauvre 50 qui craignait de faire tapisserie ! 01 + 02 + 03 + ... + 49 + 50 + 51 + 52 + ... + 97 + 98 + 99 99 + 98 + 97 + ... + 51 + 50 + 49 + 48 + ... + 03 + 02 + 01 Deux fois la somme de tous ces nombres c'est 99 fois la somme de 1 et 99... On tient la règle générale et c'est une vision géométrique qui permet de synthétiser : On a opéré une sorte de changement de cadre comme disent les didacticiens. Cette façon d'opérer était connue des Grecs, qui inventèrent les nombres géométriques ; ces nombres les ont même tout à fait passionné à la suite de Pythagore (penser au théorème éponyme et aux triades dites pythagoriciennes). Voir, par exemple, le site de Gérard Villemin pour plus d'infos.

B1/ La trilogie 2002 du calcul à l'école

Les programmes 2002 introduisent une réflexion de fond sur le calcul. Certains aspects sont développés dans des documents d'application ou d'accompagnement. On retiendra :que le calcul peut-être automatisé, réfléchi, instrumenté.
Bien entendu, à l'école primaire, il n'y a pas d'autre calcul que numérique ! Cf. supra.
L'opposition "calcul exact" / "calcul approché" n'apparait pas directement dans ces textes, et ce pour deux raisons :
1/ le calcul exact suppose une capacité algébrique (nomination de grandeurs, appels à, et calculs sur, des variables symboliques ...) et 2/ le glissement au calcul approché suppose une maitrise des nombres (des types de nombres) manipulés, ce qui n'est pas encore le cas, même pour des élèves de CM2 : pour ne prendre qu'un exemple, toute discussion sur le nombre Pi et ses approchantes -3,14 22/7 355/113 - risque d'être de peu d'effets.
En revanche, la notion de précision d'un calcul - sous couvert d'emploi d'une calculette- et donc celle de calcul approchée sont prises en charge à l'occasion de la définition des calculs réfléchi ou instrumenté.
Voici quelques commentaires très rapides, le fond du sujet devant être abordé dans la page [Calcul mental ou réfléchi].
Le calcul automatisé :

¤ s'appuie sur des automatismes de calcul
¤ suppose une restitution immédiate de tables (au sens large) dans le cas de calculs simples
¤ passe par des calculs en ligne quand c'est possible...
¤ ... ou des calculs en colonne sinon.
On voit que la maitrise des algorithmes opératoires -les fameuses opérations posées- reste incontournable.

Exemples de calculs en ligne :

25 x 8 mais pas 25 x 7 (qui relèvera du calcul réfléchi : 700 divisé par 2 deux fois).
27 + 32 voire 65 + 48 mais pas 578 + 1046.
102 + 612 mais pas 671 + 549.
4824 ÷ 12 ou 33033033 ÷ 11 mais pas 7171 ÷ 17 ...

Le calcul réfléchi :

¤ s'appuie sur certains automatismes de calcul, mais pas nécessairement tous. D'où 3 remarques :
1/ L'élève peut donc reconstituer des faits numériques manquant en s'appuyant sur les propriétés connues des opérations.
2/ les démarches de calcul sont en général diverses. C'en est même l'intérêt sur le plan pédagogique.
3/ Le calcul mental appartient à cette catégorie, étant entendu que la capacité de l'enfant à restituer des faits numériques devient prépondérante (l'apprentissage des tables reste de mise).

Illustration : un élève qui ne se souvient plus du résultat de 7x8 peut profiter de la distributivité pour calculer 7x7 + 7. De même, toute la table de 9 se retrouve grâce à la soustraction : 9 fois 17, c'est 170 moins 17, et donc 173 moins 20 ...
Le calcul instrumenté :

¤ intègre l'ensemble des dispositifs de calcul -dits modernes : calculatrice, ordinateur (tableur).
¤ libère le calculateur a priori, ou lui donne plus de pouvoir, à condition de maîtriser ... D'où 3 axes de travail avec les élèves :
1/ la maitrise de ces outils de calcul soulage dans le cas de la résolution de problèmes, à condition d'en contrôler l'usage ;
2/ on tient là des outils puissants d'exploration de faits numériques ;
3/ on peut proposer ces outils aux élèves à titre d'outils de vérification ou même de support d'exercices, par exemple lors de séances de calcul réfléchi.

B2/ La refondation 2008

On ne se livrera pas ici à une analyse des textes 2008. On se contente de noter que ceux-ci ont profondément modifié les orientations précédentes. Un indice : les textes maigrissent, les documents annexes, écrits par des experts associés à la réflexion du Ministère disparaissent, comme les experts d'ailleurs.
On se contente de repérer que ces textes mettent l'accent sur :

¤ le calcul mental (dans un sens restrictif) ;
¤ le calcul posé (ou en ligne, "éventuellement" a-ton envie d'ajouter) ;
¤ le calcul instrumenté à bon escient (sic).

Autant les textes 2002 pariaient sur l'intelligence et les capacités calculatoires des enfants, en comptant sur un fort investissement des enseignants, autant les textes 2008 semblent appeler une obligation de résultats -qui s'en plaindra ?- mais a minima, en invoquant une espèce de tradition.

Ce jugement, trop rapide certainement, ne doit pas émouvoir l'étudiant qui lira cette page. On attend de lui, à l'épreuve de mathématiques du concours de recrutement, qu'il puisse mener des calculs de façon experte, de façon bien plus experte que ce qu'on l'on attend d'un élève de CM2 voire de collège.
Les qualités de précision et de rigueur, de souplesse et d'endurance, d'anticipation et de vérification, qu'il aura pu manifester alors, ne lui seront pas de trop, quand, ayant embrassé la carrière, il devra user de méthodes expertes pour traiter rapidement les situations numériques que sa préparation de séquence lui suggérera de proposer à ses élèves.

Dernière mise à jour : 5/09/2011

[Retour Haut de la fenêtre]